2.2. Логические операции.

2.1. Основные понятия.         2.3. Логические формулы

Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение.

Выделяют следующие логические операции: инверсия;  конъюнкция; дизъюнкция, импликация; эквиваленция

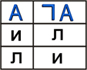
1. Операция инверсия (отрицание):

Отрицание - это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.

Обозначается:  

В естественном языке: соответствует словам "неверно, что..." и частице "не"

Диаграмма Эйлера-Венна:

Принимаемые значения:    

Диаграмма Эйлера-Венна:

В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.е. множеству получившемуся в результате отрицания множества соответствует множество, дополняющее его до универсального множества.

Пример: Луна — спутник Земли (А). Луна — не спутник Земли ( A)

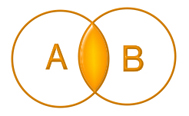
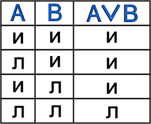
2. Операция конъюнкция (лат. conjunctio — соединение) (логическое умножение):

Конъюнкция - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Обозначается:  

В естественном языке: соответствует союзу "и"

Принимаемые значения: 

Диаграмма Эйлера-Венна:

В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.

Примеры:

  1. 10 делится на 2 (A - и). 5 больше 3 (B - и). 10 делится на 2 и 5 больше 3 (A B - и).
  2. 10 не делится на 2 (A - л). 5 больше 3 (B - и). 10 не делится на 2 и 5 больше 3 (A B - л).
  3. 10 делится на 2 (A - и). 5 не больше 3 (B - л). 10 делится на 2 и 5 не больше 3 (A B - л).
  4. 10 не делится на 2 (A - л). 5 не больше 3 (B - л). 10 делится на 2 и 5 больше 3 (A B - л).

3. Операция дизъюнкция (лат. disjunctio — разделение) (логическое сложение):

Дизъюнкция - это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.

Обозначается:  

В естественном языке: соответствует союзу "или"

Принимаемые значения:   

Диаграмма Эйлера-Венна:

В алгебре множеств дизъюнкции соответствует операция объединения множеств, т.е. множеству получившемуся в результате сложения множеств А и В соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В.

Примеры:

  1. 10 делится на 2 (A - и). 5 больше 3 (B - и). 10 делится на 2 или 5 больше 3 (A B - и).
  2. 10 не делится на 2 (A - л). 5 больше 3 (B - и). 10 не делится на 2 или 5 больше 3 (A B - и).
  3. 10 делится на 2 (A - и). 5 не больше 3 (B - л). 10 делится на 2 или 5 не больше 3 (A B - и).
  4. 10 не делится на 2 (A - л). 5 не больше 3 (B - л). 10 не делится на 2 или 5 не больше 3 (A B - л).

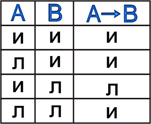
4. Операция импликация ( лат. implico — тесно связаны)

Импликация - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.

Обозначается:  

В естественном языке: соответствует обороту "если ..., то ..."

Принимаемые значения:   

Примеры:

  1. Данный четырёхугольник — квадрат (A - и). Около данного четырёхугольника можно описать окружность (B - и). Если данный четырёхугольник квадрат, то около него можно описать окружность (A B - и).
  2. Данный четырёхугольник — не квадрат (A - л). Около данного четырёхугольника можно описать окружность (B - и). Если данный четырёхугольник не квадрат, то около него можно описать окружность (A B - и).
  3. Данный четырёхугольник — квадрат (A - и). Около данного четырёхугольника нельзя описать окружность (B - л). Если данный четырёхугольник квадрат, то около него можно описать окружность (A B - л).
  4. Данный четырёхугольник — не квадрат (A - л). Около данного четырёхугольника нельзя описать окружность (B - л). Если данный четырёхугольник не квадрат, то около него нельзя описать окружность (A B - и).

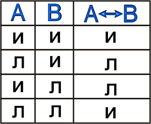
5. Операция эквиваленция (двойная импликация):

Эквиваленция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.

Обозначается:     

В естественном языке: соответствует оборотам речи "тогда и только тогда"; "в том и только в том случае"

Принимаемые значения:    

Примеры:

  1. 24 делится на 6 (A - и). 24 делится на 3 (B - и). 24 делится на 6 тогда и только тогда, когда 24 делится на 3 (A B - и).
  2. 24 не делится на 6 (A - л). 24 делится на 3 (B - и). 24 не делится на 6 тогда и только тогда, когда 24 делится на 3 (A B - л).
  3. 24 делится на 6 (A - и). 24 не делится на 3 (B - л). 24 делится на 6 тогда и только тогда, когда 24 делится на 3 (A B - л).
  4. 24 не делится на 6 (A - л). 24 не делится на 3 (B - л). 24 не делится на 6 тогда и только тогда, когда 24 не делится на 3 (A B - и).
Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания (“не”), затем конъюнкция (“и”), после конъюнкции — дизъюнкция (“или”) и в последнюю очередь — импликация и эквиваленция.   вывод формулы
Hosted by uCoz